Long time no see! I had a very busy couple of months (finishing a paper, abstracts to conferences, surgery, immigration processes, etc.), but I’m back to talk about genotype-phenotype association studies.
To understand genotype-phenotype studies like Genome-Wide Association Studies (GWAS) the first thing you need to understand is the premise.
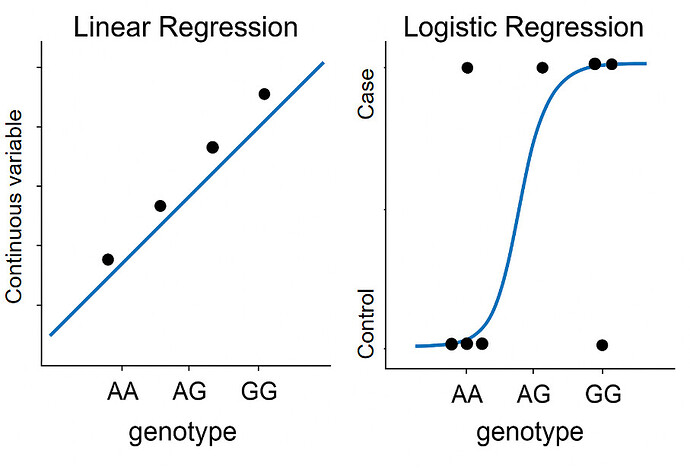
For discrete phenotypes (like case-control studies), the idea is simple: if a genetic variant is associated with your condition, it should appear more frequently in cases than in controls. For continuous phenotypes (like height), you expect individuals carrying certain variants to consistently have higher or lower values of the trait compared to those without the variant. In terms of analysis, we typically use Logistic regression for discrete outcomes (e.g., disease status: case vs. control), and Linear regression for continuous outcomes (e.g., height, blood pressure).
Figure 1: Linear and Logistic regression in GWAS. Challenge: Please explain how I have a point that is between AA and AG on Logistic Regression.
In genetic epidemiology, we generally prefer regression models over other methods because they allow us to include covariates. For example, a Chi-square test does not allow you to adjust for covariates, meaning you can’t control for potential biases caused by other variables beyond allele information. Imagine studying Parkinson’s disease and perform analysis without accounting for age in your model: this would be bizarre and could easily lead to misleading conclusions.
Until today, all PD GWAS papers I’ve seen used age, sex, and genetic principal components (PCs) as covariates. For selecting PCs, I’ve noticed two main approaches: (i) Including a fixed number of PCs, usually 5 or 10 or (ii) Using feature selection methods, like stepwise AIC, to decide which PCs to include.
This second method has received some criticism, as it may include variables that aren’t relevant or exclude variables that are important.
Besides that, regression provides summary statistics that make it easier to interpret the findings. The most common ones are the beta coefficient, odds ratio (OR), 95% confidence interval (CI), and p-value.
-
Beta coefficient: Used in linear regression. It tells you how much the phenotype increases or decreases with each additional copy of the allele. A positive beta means the allele is associated with higher values of the trait, and a negative beta means lower values.
-
Odds Ratio (OR): Common in logistic regression, it shows how much more (or less) likely the outcome is to occur in individuals with the allele compared to those without it. An OR above 1 means increased risk; below 1 means decreased risk. You can convert Beta to OR and OR to Beta.
-
Standard error (SE): SE quantifies the uncertainty in estimated effect sizes, such as beta coefficients or odds ratios, for each variant. Smaller standard errors indicate more precise estimates, implying a smaller range of plausible values for the true effect, while larger standard errors suggest greater uncertainty and a wider range of possible true effects.
-
95% Confidence Interval (CI): A range of values that likely contains the true effect size (beta or OR) 95% of the time. If the CI crosses 0 (for beta) or 1 (for OR), the result is usually considered not statistically significant.
-
p-value: The p-value tells you how likely it is to see the association you found (or something more extreme) just by random chance if there were actually no real association (the null hypothesis is true). A small p-value (typically < 0.05) suggests that the result is unlikely to be due to chance, providing evidence for a real association
So, does that mean if I run a GWAS, all variants with p < 0.05 are statistically significant? Unfortunately, no. In GWAS, we usually apply something called Bonferroni correction. The logic is simple: if you test enough variants, some p< 0.05 will appear significant purely by chance. To account for this, we adjust our significance threshold by dividing the standard p-value cutoff (0.05) by the number of independent tests. For the human genome, we commonly use around 1,000,000 independent tests as a rough estimate, which gives us the famous genome-wide significance threshold of 5 × 10⁻⁸.
The easiest way to visualize GWAS results is through the Manhattan plot and the QQ plot.
Figure 2: Manhattan plot from Leal et al. 2025 (preprint)
The Manhattan plot shows each variant as a point, with the x-axis representing the chromosome and base pair position, and the y-axis representing the −log10(p-value).
A horizontal line indicates the p-value threshold. Typically, Manhattan plots include either:
-
One line for genome-wide significance (5 × 10⁻⁸), or
-
Two lines: one for genome-wide significance (5 × 10⁻⁸) and another for suggestive significance (1 × 10^-6 ).
Another commonly used plot in GWAS is the QQ plot. Personally, I’m a bit of a “QQ plot hater” — mainly because it’s easy to misinterpret the plot if you don’t clearly understand what the observed and expected p-values represent.
So, the observed p-value is straightforward — it’s just the p-value you get from your GWAS.
But how do you get the expected p-value in a QQ plot?
The expected values are not based on your data, but rather on the rank of p-values under the null hypothesis. That means the QQ plot depends only on the number of variants tested in your GWAS.
Let’s say your GWAS has 10,000 variants. The QQ plot assumes that, under the null (i.e., no true associations), the p-values follow a uniform distribution. So you expect: 1 variant to have p ≤ 1/10,000; 2 variants to have p ≤ 2/10,000; 3 variants to have p ≤ 3/10,000; … ; 5,000 variants to have p ≤ 5,000/10,000 (= 0.5); … ; 10,000 variants to have p ≤ 10,000/10,000 (= 1). If your GWAS was well done (i.e., no inflation or confounding), the points will follow the diagonal. Systematic deviation from the diagonal could suggest population stratification, relatedness, technical artifacts, or even real associations.
Now imagine your GWAS includes 10 million samples. With such a huge sample size, even very small genetic effects will produce extremely low p-values. In this case, you might interpret some signals as problematic (e.g., inflation or overfitting), when in fact they’re just a consequence of high power. On the other hand, if you have a very small sample size, your GWAS will be underpowered, meaning you won’t have enough statistical power to detect real associations.
There’s also the most extreme scenario: your phenotype is not genetically driven at all. For example, imagine doing a GWAS for whether someone watched a solar eclipse. In this case, your study is severely underpowered not just because of sample size, but because there’s nothing genetic to find.
When you’re in such low-power situations, there’s a temptation to remove variables from your model, thinking you’re overfitting. But sometimes, it’s not about model complexity — it’s just that there’s no genetic signal to detect.
Figure 3: QQPlot from Leal et al. 2025 (preprint)
Another important metric is the genomic inflation factor (λGC), which compares the observed and expected p-values from your GWAS.
I won’t go into the details of how it’s calculated because it involves chi-square distributions and degrees of freedom, and I’m not explaining those today.
In simple terms, λGC can fall into three general categories:
- λGC = 1 → No inflation
- λGC > 1 → Potential inflation
- λGC < 1 → Possible deflation, which might suggest overfitting
If λGC is only slightly above 1 (like 1.01 or 1.02), it’s usually nothing to worry about.
But if it’s clearly elevated — for example, 1.1 or higher — that’s a signal to revisit your model and check whether it properly accounts for population structure, relatedness, or other confounders.
This post was just a quick introduction to GWAS because in my next post, I’ll dive into the results of my own paper (currently on preprint!). I’ll go over some of the models we used, show a few key plots, and there will be memes. This memeless post was really sad.